Висота ромба дорівнює 12 см а одна з його діагоналей 15 см знайти площу ромба

Question

Висота ромба дорівнює 12 см а одна з його діагоналей 15 см знайти площу ромба

Answer 1

Н = 12см
Д = 15 см
проекция диагонали на нижнюю сторону равна Пр = √(Д² - Н²) =√(15² + 12²) = 9
Сторона, на которую опущена высота, делится основанием высоты на два отрезка: один - Пр = 9, другой а - Пр = (а - 9)
Теперь посмотрим  на треугольник, образованный боковой стороной,  высотой и отрезком (а - 9)
а² = (а - 9)² +  12²
а² = а² - 18а + 81 + 144
18а = 225
а = 12,5
Вот и до площади добрались
S  = а ·Н = 12,5·12 = 150(см²)

Answer 2

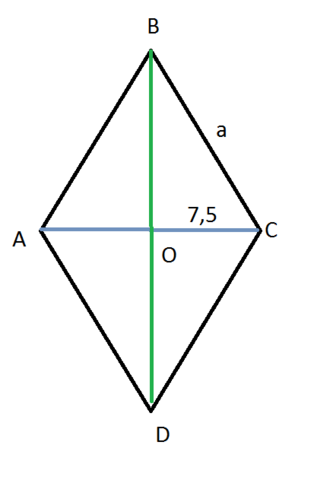
Из треугольника ВОС
ВО²=ВС²-ОС²=а²-7,5²=а²-56,25
S(ромба)=a·h=12a
S(ромба)=d₁·d₂/2=15·2√(a²-56,25)/2=15√(a²-56,25)
Уравнение
12а=15√(a²-56,25)
 4а=5√(a²-56,25)
Возводим в квадрат
16а²=25(а²-56,25)
9а²=25·56,25
a=5/3·√56,25
a=5/3·√(225/4)=25/2
S=12a=12· (25/2)=150 кв см

---