Ответ:
3,125 см.
Объяснение:
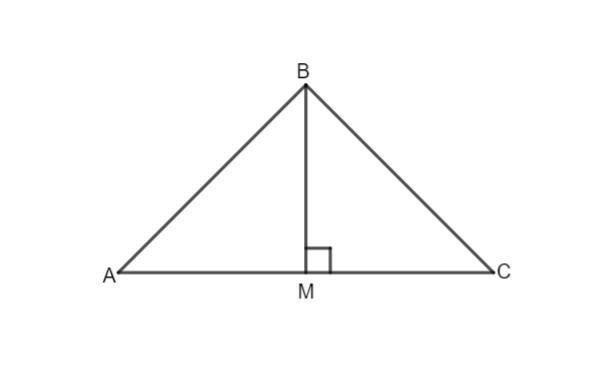
ΔАВС - равнобедренный;
АВ=ВС = 5 см;
ВМ - высота;
ВМ= 4 см;
Радиус окружности, описанной около треугольника находится по формуле:

где  - угол противолежащий стороне а.
- угол противолежащий стороне а.
Рассмотрим Δ АВМ - прямоугольный.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Тогда

Тогда найдем радиус окружности, описанной около ΔАВС .