Ответ:
S ABC = 16.5 см²
S ABCD = 33 см²
Объяснение:
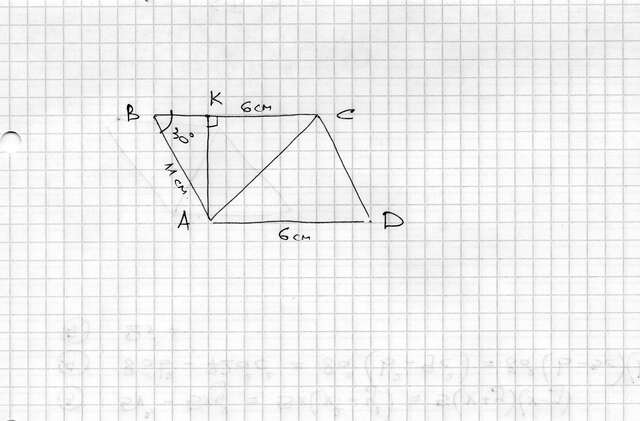
1. Опустим из точки A высоту на ВС получит точку К
2. Треугольник ABE будет прямоугольным, угол B в котором равен 30° (по условию).
По свойствам прямоугольных треугольников, катет AK лежащий напротив угла в 30° равен половине гипотенузы AB
AK = AB/2 = 11/2 = 5.5 см
Площадь параллелограмма равна произведению основания на высоту опущенную к основанию. Основание в нашем случае BC, высота AК
S ABCD = BC*AК = 6*5.5 = 33 см²
Площадь треугольника ABC равна половине площади параллелограмма:
33/2 = 16.5 см²