Ответ:
Каждая точка биссектрисы угла равноудалена от сторон угла.
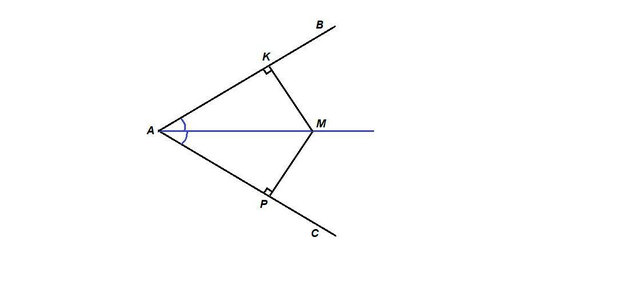
Дано: ∠ВАС, АМ - биссектриса,
Доказать: d(M, BA) = d(M, CA).
Доказательство:
Проведем МК⊥АВ и МР⊥АС.
МК - расстояние от точки М до АВ, т.е. d(M, AB) = MK,
MP - расстояние от точки М до АС, т.е. d(М, АС) = МР.
Докажем, что МК = МР.
Рассмотрим треугольники АКМ и АРМ:
∠АКМ = ∠АРМ = 90°,
∠КАМ = ∠РАМ, так как АМ - биссектриса,
АМ - общая сторона, ⇒
ΔАКМ = ΔАРМ по гипотенузе и острому углу.
Значит, МК = МР, что и требовалось доказать.