Срочно!!!! Дана трапеция ABCD (AD||BC), диагонали трапеции пересекаются в точке О,...

Ответ:

$S_{ABCD}= 36~ cm^{2}$

Объяснение:

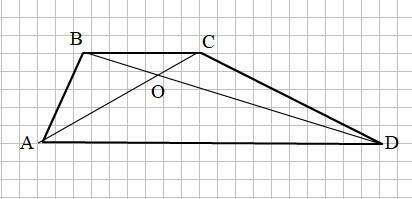
Смотри прикреплённый рисунок.

Известно, что диагонали трапеции делят трапецию на 4 треугольника, площади которых находятся в следующем соотношении:

$S_{BOC} \cdot S_{AOD}=S_{AOB}\cdot S_{COD}$ (1)

$S_{BOC} = 4~cm^{2};$

$S_{COD} = 8~cm^{2};$

Найдём площадь ΔСOD.

$S_{\Delta ABD} = S_{\Delta ACD}$ , так как эти треугольники имеют одно и то же основание AD и одинаковые высоты, равные высоте трапеции.

$S_{ABD} = S_{AOB} + S_{AOD};~~~S_{ACD} = S_{COD} + S_{AOD};$

Таким образом

$S_{AOB} + S_{AOD} = S_{COD} + S_{AOD};$

$S_{AOB} = S_{COD} = 8~cm^{2}$ .

Из соотношения (1) найдём площадь ΔAOD.

$S_{AOD}= \dfrac{S_{AOB}\cdot S_{COD}}{S_{BOC}} = \dfrac{8\cdot 8}{4} = 16 ~(cm^{2} )$

Площадь трапеции ABCD равна

$S_{ABCD}= S_{AOB} + S_{BOC}+S_{COD}=S_{AOD} = \\\\ = 8 + 4 + 8 + 16 = 36~ (cm^{2})$