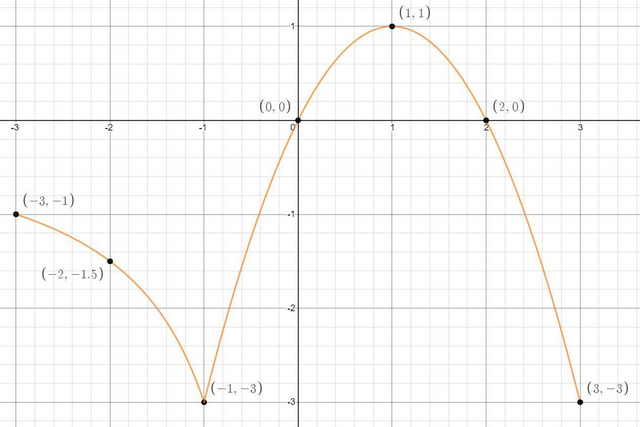
Первая функция это гипербола, асимптоты которой y= 0 и x=0, график лежит в 1 и 3 четверти относительно своих асимптот, функция не пересекает оси координат т.к. они являются её асимптотами. Найдём координаты границ и середины отрезка на котором функция существует, он достаточно маленький.

Вторая функция это парабола, ветви которой направлены вниз, координата вершины (1;1), пересекает оси координат в точках: (0;0) и (2;0). Найдём границы отрезка на котором функция существует.

Как видно границы совпадают, поэтому на отрезке [-3;3] функция непрерывная.
Используя данные, что мы нашли построим график общей функции, помня о том как выпукла парабола и гипербола.