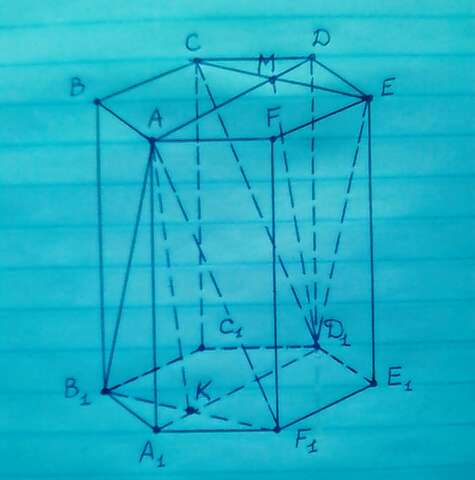
РЕШЕНИЕ:
1) Прямые AB1 и CD1 расположены в параллельных плоскостях:
( AB1F1 ) || ( CED1 ) по признаку параллельности двух плоскостей: две пересекающиеся прямые AB1 и АF1 плоскости AB1F1 соответственно параллельны двум пересекающимся прямым ED1 и СD1 плоскости CED1
2) Все боковые грани правильной шестиугольной призмы равны
Значит, ∆ AB1F1 - равнобедренный, АВ1 = АF1
3) АА1 перпендикулярен А1D1 ( AA1 - высота призмы )
A1K перпендикулярен В1F1 ( по свойству правильного шестиугольника A1D1 перпендикулярен В1F1, к тому же A1D1 делит отрезок В1F1 пополам => B1K = F1K )
Значит, по теореме о трёх перпендикулярах
АК перпендикулярен В1F1 ( или это можно доказать через свойство правильного шестиугольника, которое привёл выше )
АК - высота, медиана, биссектриса
4) Рассмотрим ∆ АА1F1 ( угол АА1F1 = 90° ):
По теореме Пифагора:
АF1² = AA1² + A1F1²
AF1² = 12² + 10² = 144 + 100 = 244
AF1 = 2√61
5) Рассмотрим ∆ А1KF1 ( угол A1KF1 = 90° ):
Все углы правильного шестиугольника равны 120°
угол А1F1K = 120° - 90° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы
А1К = 1/2 × А1F1 = 1/2 × 10 = 5
По теореме Пифагора:
A1F1² = A1K² + KF1²
A1K² = 10² - 5² = 100 - 25 = 75
A1K = 5√3 => B1F1 = 2 × KF1 = 2 × 5√3 = 10√3
6) Рассмотрим ∆ АА1К ( угол АА1К = 90° ):
По теореме Пифагора:
АК² = А1К² + АА1²
АК² = 12² + 5² = 144 + 25 = 169
АК = 13
7) Большая диагональ правильного шестиугольника в два раза больше его стороны =>
А1D = 2 × A1B1 = 2 × 10 = 20
KD1 = A1D1 - A1K = 20 - 5 = 15
8) Плоскости АВ1F1 и CED1 параллельны
Плоскости оснований призмы также параллельны
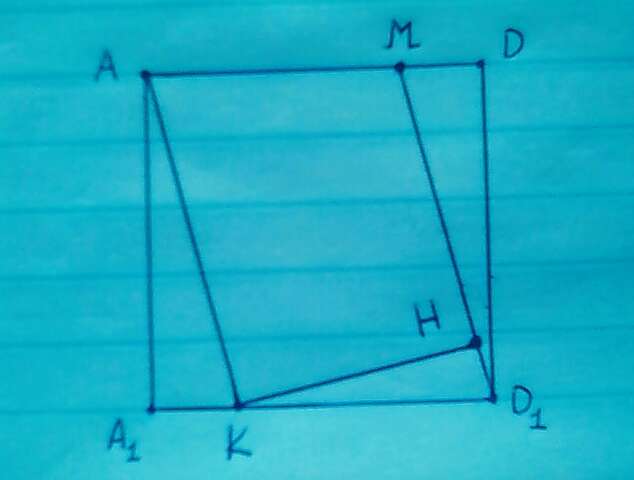
Из этого следует, что четырёхугольник АKD1M - параллелограмм
Значит, отрезок КН, то есть высота параллелограмма, перпендикулярна плоскостям АВ1F1 и CED1 и является искомым
9) Площадь параллелограмма равна произведению основания на его высоту
S = a × h = AA1 × KD1 = 12 × 15 = 180
Но с другой стороны площадь параллелограмма равна:
S = MD1 × KH
180 = 13 × КН
КН = 180 / 13
Значит, расстояние между плоскостями AB1F1 и CED1, равное расстоянию между прямыми АВ1 и CD1, равно 180 / 13
ОТВЕТ: 180 / 13