Дано:треугольник BCA, BM=MA, A=50°,CM=6 см,CM биссектриса Найти АB Углы BCM AMC

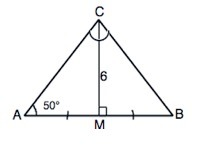
По условию СМ - биссектриса, АМ=ВМ, ⇒ СМ - медиана.

Если биссектриса угла в треугольнике совпадает с медианой, то она – высота и перпендикулярна стороне, противолежащей тому углу и делит треугольник на два прямоугольных треугольника.

В ∆АСМ и ∆ ВСМ катеты АМ=ВМ по условию, СМ - общая сторона. ⇒

∆АСМ = ∆ ВСМ, ⇒АС=ВС, поэтому ∆ АСВ равнобедренный.

∆ АСМ - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°. ⇒∠АСМ=90°-50°=40°

По т.синусов

$\frac{CM}{sin50 ^{o}} = \frac{AM}{sin40^o} } }$

Значения синусов найдем в таблице Брадиса или с помощью инженерного калькулятора.

6:0,7660=АМ:0,6428

АМ=5,035

АВ=2 АМ=10,07 (ед.длины)