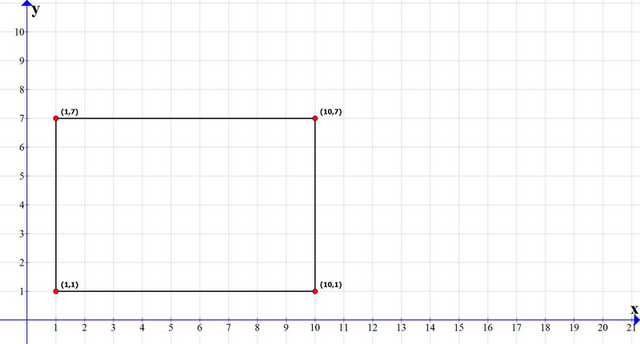
1) Две точки прямоугольника- (1;1), (10;1) расположены на высоте 1 (то есть, координата y=1).
Ещё две точки (1;7), (10;7) расположены на высоте 7 (то есть, координата y=7).
Расстояние по оси y между этими парами точек равно a = 7 - 1 = 6.
Это первая сторона прямоугольника.
Расстояние по оси x между точками в каждой паре равно b = 10 - 1 = 9.
Это вторая сторона прямоугольника.
Перемножив стороны, найдём площадь этого прямоугольника:
S = a * b = 6 * 9 = 54
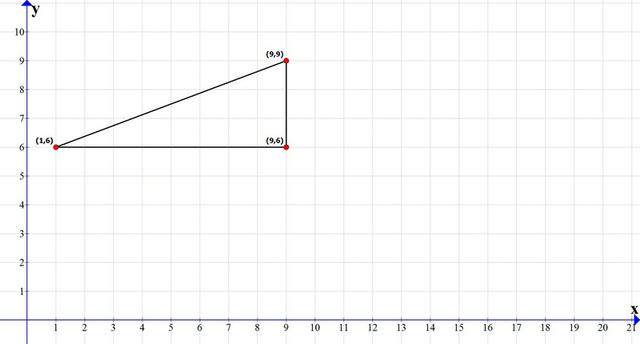
2) В этом треугольнике сторона с вершинами (1;6), (9;6) параллельна оси x, так как точки имеют одинаковую координату y.
А сторона с вершинами (9;6), (9;9) - параллельна оси y, так как точки имеют одинаковую координату x.
Следовательно, угол между этими сторонами- прямой. Значит, наш треугольник- прямоугольный, а эти стороны являются его катетами.
В прямоугольном треугольнике площадь равна половине произведения катетов.
Длина первой стороны равна разности координат x первой пары точек:
a = 9 - 1 = 8
Длина второй стороны равна разности координат y второй пары точек:
b = 9 - 6 = 3
Вычислим площадь треугольника:
S = a * b / 2 = 8 * 3 / 2 = 12
Для наглядности, приложу картинки с этими фигурами, построенными в системе координат.