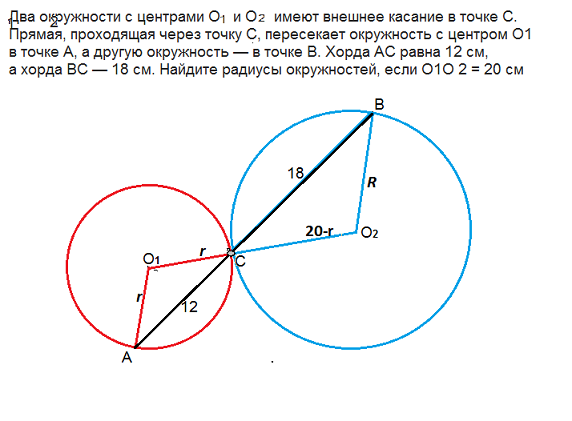
Задача на подобие треугольников.
Пусть радиус меньшей окружности будет r, тогда радиус большей R=20-r см
Центры касающихся окружностей лежат на одной прямой, проходящей через точку касания окружности; прямая АВ проходит через ту же точку, что и отрезок, соединяющий центры окружностей.
В треугольниках АО₁С и ВО₂ углы при С равны, значит, их углы при А и В тоже равны, т.к. являются углами при основании равнобедренных треугольников, образованных радиусами окружностей как боковыми сторонами.
.Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Из подобия треугольников
АС:СВ=r:(О₁О₂-r)
12:18=r:(20-r)
12*(20-r)=18r
240=30r
r=8 см
R=20-8=12 см