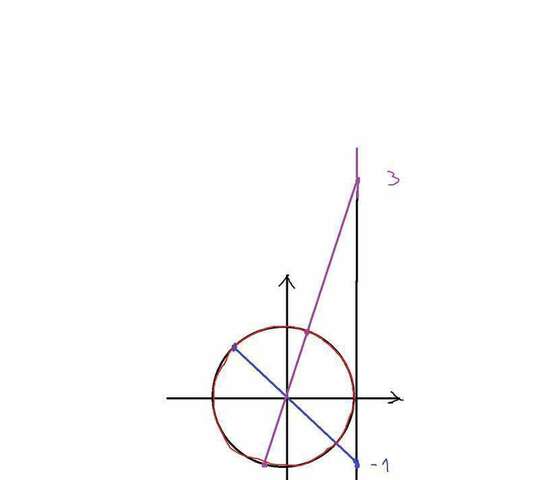А) Для начала представим 3 в правой части уравнения как 3*1 = 3(sin^2 x + cos^2 x) = 3sin^2 x + 3cos^2 x. Здесь я воспользовался тем, что 1 = sin^2 x + cos^2 x.
Переносим всё влево и приводим подобные слагаемые:
4sin^2 x - 2sinx * cos x - 3sin^2 x - 3cos^2 x = 0
sin^2 x - 2sinx * cos x - 3cos^2 x = 0
Для дальнейшего решения разделим обе части уравнения на cos^2 x. Почему это можно сделать? Мы ведь знаем, что делить имеем право лишь на выражение, нигде не равное 0. Уверены ли мы, что cos^2 x не равен нигде 0? Так и есть. Убедимся в этом. Пусть cos x = 0. Тогда
sin^2 x - 0 - 0 = 0
sin^2 x = 0, откуда sin x = 0. Но это невозможно! Ибо в силу соотношения sin^2 x + cos^2 x = 1, если cos x = 0, то синус обязан равняться 1.Противоречие с полученным. Итак, cos x не равен 0, значит, и cos^2 x не равен 0. Делим на него:
tg^2 x - 2tg x - 3 = 0
думаю, понятно, откуда мы получили tg x(tg x = sin x / cos x)
Теперь вводим замену. Пусть tg x = t
С учётом замены:
t^2 - 2t - 3 = 0
t1 = 3; t2 = -1
Вспоминая, что t = tg x, получаем два уравнения:
tg x = 3 или tg x = -1
x = arctg 3 + пиn x = -пи/4 + пиk
Здесь n и k - целые числа.
Таким образом, получаем ответ.
Теперь ответим на второй вопрос задачи. Существует несколько способом отбора корней. Мы воспользуемся отбором по тригонометрическому кругу. Сейчас приложу рисунок.
Вкратце о том, что мы делаем. Я решил графически уравнения tg x = -1 и tg x = -3.
Значения тангенсов находятся на оси тангенсов(Вы видите её на рисунке - это касательная, параллельная оси ординат).
Наносим на ней точки -1 и 3(по какому принципу отмечал, тоже, думаю, можно догадаться).
Проводим через них прямые, проходящие через центр окружности, до пересечения с окружностью. В каждом случае получаются две такие точки - это и есть решения уравнений. Решения каждого уравнения я отметил разными цветами.
После этого начинаем двигаться от точки 0, и записывать названия точек, встретившихся нам на пути по заданному интервалу(до 2пи). Как это делать - вопрос совершенно иной, и я его здесь не обсуждаю. Так или иначе, получаем, что интервалу принадлежат следующие корни:
arctg 3; 3пи/4; пи + arctg 3; 7пи/4
Из них наибольшим углом является 7пи/4 - это очень хорошо видно по окружности(точка находится дальше всех от 0).
Учитывая, что пи - это 180 градусов, получаем, что
7пи/4 = (7 * 180) / 4 = 315 градусов