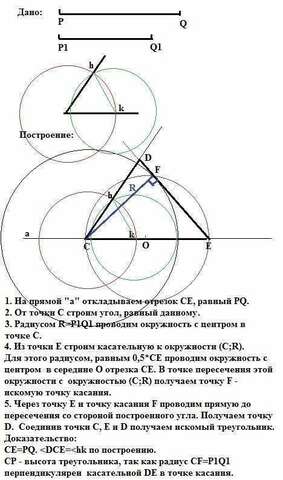
1. На прямой "а" откладываем отрезок СЕ, равный PQ.
2. От точки С строим угол, равный данному (ясно из рисунка)
3. Радиусом R=P1Q1 проводим окружность с центром в точке С.
4. Из точки Е строим касательную к окружности (С;R).
Для этого радиусом, равным 0,5*СЕ проводим окружность с центром в середине О отрезка СЕ. В точке пересечения этой окружности с окружностью (С;R) получаем точку F - искомую точку касания.
5. Через точку Е и точку касания F проводим прямую до пересечения
со стороной построенного угла. Получаем точку D.
Соединив точки С, Е и D получаем искомый треугольник.
Доказательство:
СЕ=PQ. СF - высота треугольника, так как радиус CF=P1Q1 перпендикулярен
касательной DE в точке касания.