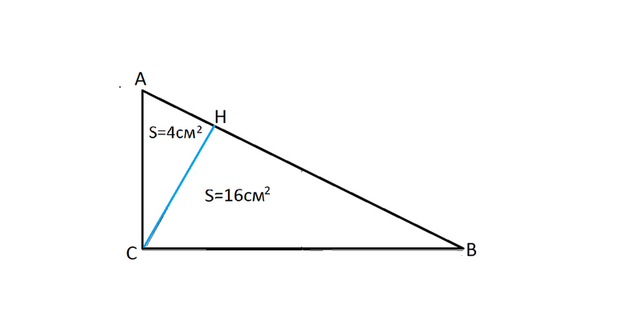
Высота прямоугольного треугольника, проведенная из прямого угла к гипотенузе, делит его на подобные треугольники.
Пусть будет треугольник АВС, СН - высота к гипотенузе.
Тогда отношение площадей треугольников АСН и ВСН
S₁:S₂ =т 4:16 или 1/4.
Так как
отношение площадей подобных фигур равно квадрату коэффициента подобия,
коэффициент подобия k= √1/4=1/2
Следовательно, гипотенузы
треугольников АСН и ВСН относятся как
1:2
Но АС и ВС - катеты треугольника АВС.
ВC=2АС
Площадь Δ АВС=АС*ВС:2
S (ABC)=(S ACH+S BCH)=4+16=20 см²
ВC=2АС
S (ABC)=АC*2 AС:2
2 S (ABC)=
2 AC²=40
AC²=20
AC=√20 см
BC=2√20 см
АВ²=АС²+ВС²
АВ²=(√20)²+( 2√20)²=20+80
АВ²=100
АВ=10 см