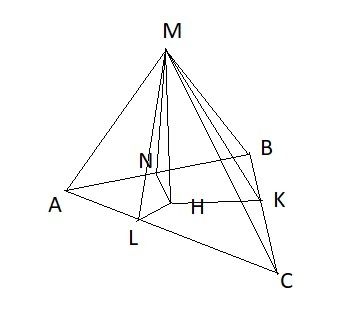
ML = MK = MN = 2
MH = 1
AB= AC = BC = ?
Т.к. прямоугольные ΔMLH = ΔMKH = ΔMNH (равны гипотенузы и MH общая), то HL = HK = HN, и следовательно H - центр вписанной окружности.
Из прямоугольного ΔMLH по теореме Пифагора:

Радиус вписанной окружности правильного треугольника выражается через его сторону: