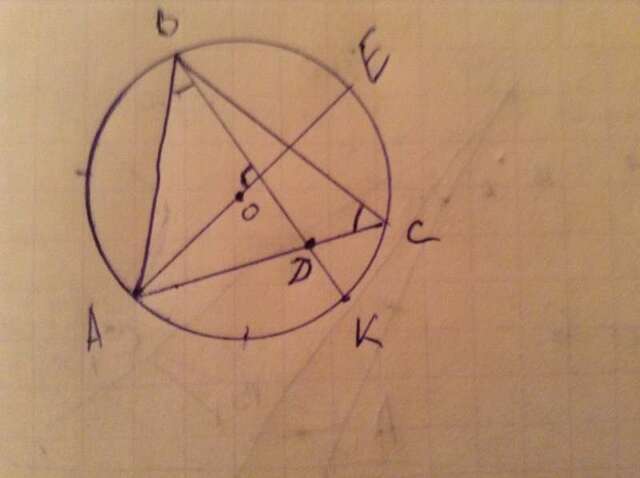Прямая BD пересекает описанную окружность в точке К, а прямая АО - в точке Е. Т.к. АО-радиус окружности, значит АЕ - ее диаметр. ВК-хорда окружности. По условию ВД перпендикулярна АО, значит и ВК перпендикулярна AЕ. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Значит, точка A — середина дуги КАВ, дуга КА равна дуге ВА. Вписанные углы, опирающиеся на равные дуги, равны, следовательно ∠АСВ=∠АВК=∠АВД. Получается у треугольников ABD и ACB два угла равны (∠А-общий), значит треугольники подобны по двум углам. Следовательно, АД/АВ=АВ/АС. АД=АВ²/АС=40²/64=25. Значит СД=АС-АД=64-25=39.