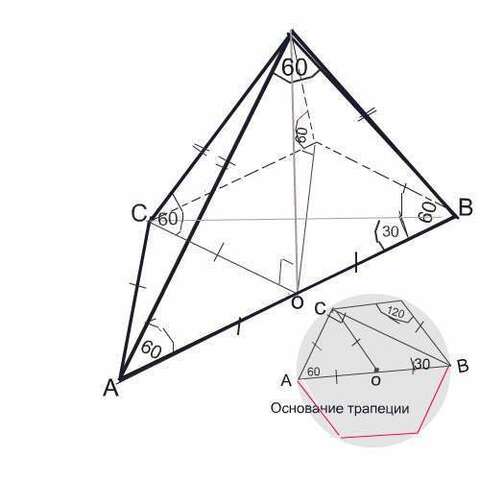
Главное в этой задаче - рисунок. Если он сделан правильно, решить ее не просто, а очень просто.
Данная в основании пирамиды трапеция равнобедренная по условию задачи.
Диагональ трапеции является биссектрисой угла 60 °. Боковая сторона ее вдвое меньше большего основания, т.к. противолежит углу 30°.
Угол, образуемый диагональю с боковой стороной трапеции у меньшего основанияя равен 90°.
Следовательно, треугольник, сторонами которого являются боковая сторона, большее основание и диагональ трапеции, - прямоугольный, медиана его равна половине большей стороны и равна боковой стороне, т.к.острый угол трапеции равен 60°.
Расстояние от центра большго основания трапеции одинаково до всех углов трапеции.
Поскольку ребра пирамиды образуют с основанием трапеции углы 60°, всю пирамиду можно представить как половину пирамиды, в основании которой лежит правильный шестиугольник, диагональное сечение которого - правильный треугольник.
Из условия задачи известно, что высота пирамиды равна 4√3.
Эта же высота 4√3 является высотой правильного треугольника, плоскость которого перпендикулярна плоскости основания пирамиды и большему основанию трапеции.
Большую сторону АВ=а трапеции можно вычислить по теореме Пифагора или из формулы высоты правильного треугольника.
4√3=а√3:2
4=а:2
а=8
Большее основание трапеции равно 8 (м, дм, см?)