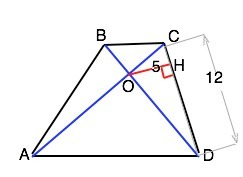
В трапеции ABCD треугольники АВD и ACD имеют общее основание и высоты, равные высоте трапеции. Следовательно, их площади равны.
S ∆ ABO=S∆ ABD - S∆ AOD;
S∆ COD=S ∆ ACD - S∆ AOD ⇒
Треугольники , образованные боковыми сторонами и диагоналями трапеции, имеют равные площади.
S ∆ ABO=S∆ COD
В ∆ СОD отрезок ОН перпендикулярен CD и является его высотой.
Формула площади треугольника
S=a•h/2
S ∆ AOB=S ∆ COD= CD•OH/2=12•5/2=30 см²