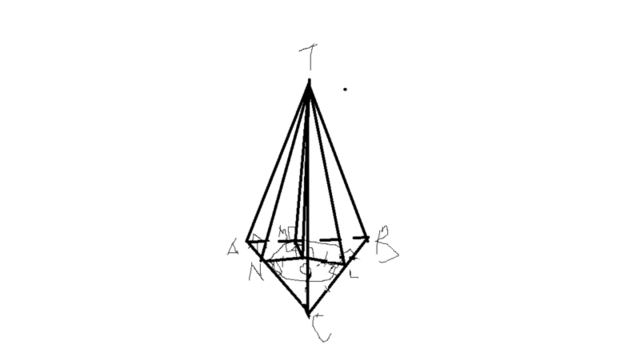
Рисунок конечно получился не очень,но надеюсь поймете:Опустим высоту пирамиды TO.По теореме о 3 перпендикулярах NO перпендикулярно AC, LO перпендикулярно CB,MO перпендикулярно AB. ТК все высоты равны между собой,то прямоугольные треугольники TON,TOL,TOM равны по общему катету
TO и равным гипотенузам,являющимися равными высотами.Тогда MO=NO=LO ,а тк они перпендикулярны сторонам треугольника,то точка O равноудаленна от сторон треугольника ABC.Это знгачит что O-центр вписанной в треугольник ABC окружности. Найдем ее радиус NO=r, TO=H
r=S/p p-полупериметр. p= (10+10+12)/2=16 S=sqrt(16*6*6*4)=sqrt(4^2*6^2*2^2)=4*6*2=48 (Формула Герона)
r=48/16=3.По теореме пифагора:H=TO=sqrt((TN)^2-r^2)=sqrt((5*sqrt(2))^2-3^2)=sqrt(41) Обьем:V=1/3 *S*H=16*sqrt(41)