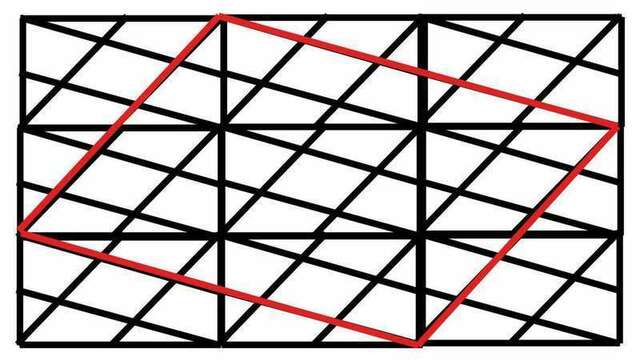
Я на рисунке расположил рядом 9 таких прямоугольников. Там слегка неаккуратно, все косые линии - прямые (не ломаные).
Внутри четырехугольника, обведенного красным, 25 одинаковых фигур, площадь которых надо найти. Их 4 треугольников, которые ЗА ПРЕДЕЛАМИ красной линии, можно сложить 4 изначальных прямоугольника (попарно - треугольники из противоположных углов прикладываются гипотенузами.
Поэтому площадь ограниченного красным параллелограмма равна 9 - 4 = 5 площади прямоугольника. Отсюда площадь параллелограмма, которую надо найти, равна 5/25 = 1/5 площади прямоугольника :))))))))))