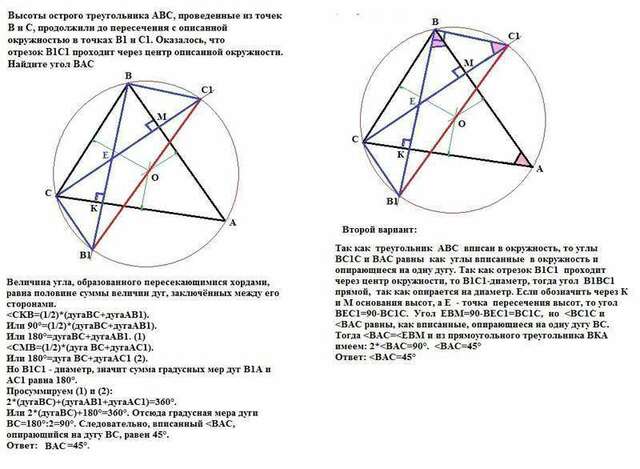
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
На приложенном рисунке
Или 90°=(1/2)*(дугаBC+дугаAB1).
Или 180°=дугаBC+дугаAB1. (1)
Или 180°=дуга ВС+дугаАС1 (2).
Но В1С1 - диаметр, значит сумма градусных мер дуг В1А и АС1
равна 180°.
Просуммируем (1) и (2):
2*(дугаВС)+(дугаАВ1+дугаАС1)=360°.
Или 2*(дугаВС)+180°=360°. Отсюда градусная мера дуги
ВС=180°:2=90°. Следовательно, вписанный <ВАС, опирающийся на дугу ВС, равен 45°.<br>Ответ: <ВАС=45°.<br>
Второй вариант:
Так как треугольник ABC вписан в окружность, то углы BС1С и BAC равны как углы вписанные в окружность и опирающиеся на одну дугу. Так как отрезок B1С1 проходит через центр окружности, то B1C1-диаметр, тогда угол В1ВС1 прямой, так как опирается на диаметр. Если обозначить через К и М основания высот, а E - точка пересечения высот, то угол ВЕС1=90-BС1C.
Угол ЕВМ=90-BEС1=BС1С, но Тогда Ответ: