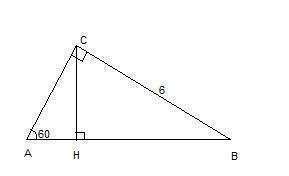
1. sin A = BC : AB, отсюда
АВ = BC : sin 60° = 6 : √3/2 = 4√3 см
2. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим неизвестный угол В:
3. В прямоугольном треуг-ке АВС катет АС, лежащий против угла В в 30°, равен половине гипотенузы АВ, значит:
АС=1/2АВ=1/2*4√3=2√3 см
4. Площадь прямоугольного треугольника равна половине произведения его катетов:
S=1/2AC*BC=1/2*2√3*6=6√3 см²
5. В прямоугольном треуг-ке ВНС катет СН (он же высота), лежащий против угла В в 30°, равен половине гипотенузы ВС, значит:
СН=1/2ВС=1/2*6=3 см