Переносим слагаемые с переменной х влево, без переменной - вправо:
ах+2х+х=1-3,
(а+3)х=-2,
при а+3≠0 можно разделить обе части уравнения на а+3, получим
х=-2/а+3 - уравнение имеет единственное решение при а≠-3
при а=-3 уравнение не имеет решений, так как делить на ноль нельзя, а уравнение принимает вид
0·х=-2
какое бы х мы ни подставили в уравнение, слева будет 0, а справа - 2.
0 =-2 - неверное равенство.
2) раскрываем знак модуля.
1 способ по определению модуля: модуль положительного выражения равен этому же самому выражению, модуль отрицательного равен выражению, взятому в противоположным знаком.
Так как выражение под модулем два, тогда придется рассмотреть 4 случая: оба подкоренных выражения больше нуля, оба меньше нуля, выражения разных знаков.
2 способ - метод промежутков:
первое подмодульное выражение меняет знак проходя через точку х=2, второе - через точку х=0.
Эти две точки разбивают числовую прямую на три промежутка:
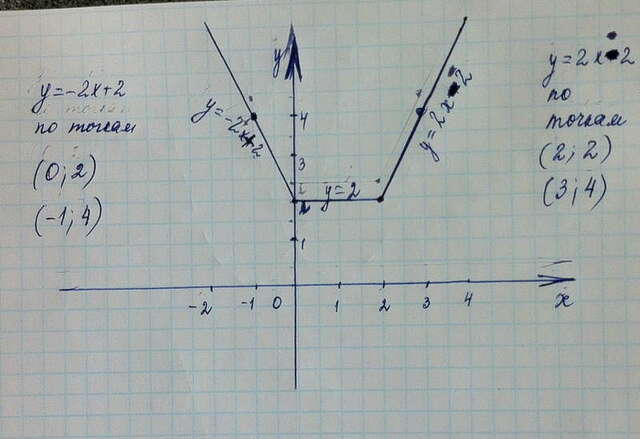
(-∞;0] х<0, x-2<0. Значит |x|=- x, |x-2|= - (x-2) тогда y=-x+2-x<br>На (-∞;0] строим график функции у=-2х+2
(0;2] x>0, x-2<0 Значит |x|=x, |x-2|=-(x-2) тогда y=-x+2+x<br>На (0;2] строим график функции у=2
(2;+∞) х>0, x-2>0. Значит |x|= x, |x-2|=x-2 тогда y=x-2+x
На (2;+∞) строим график функции у=2х-2
( cм. рисунок)