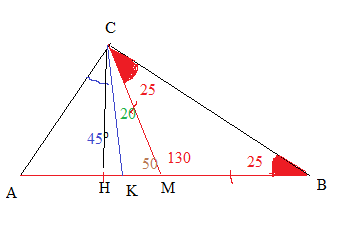
Проведем высоту СН, биссектрису СК и медиану СM ( см. рисунок)
Биссектриса делит прямой угол пополам, Значит
∠ ACK=KCB=45°
Угол между биссектрисой и медианой равен 20°, т.е ∠ KCM=20°
Значит
∠
ВСМ=45°-20°=25°
Медиана прямоугольного треугольника равна половине гипотенузы,
треугольник ВСМ- равнобедренный. углы ВСМ и МВС равны по 25 градусов, значит
∠
СМВ=180°-25°-25°=130°
смежный с ним угол АМС=180°-130°=50°
В прямоугольном треугольнике СНМ сумма острых углов равна 90°
Если один угол 50°, то второй равен 40°
∠
НСМ=40°
∠
НСК=
∠
НСМ-∠КСМ=40°-20°=20°
Ответ. 20°