Найдите область определения функцииy=

0}} \right. " alt="y= \frac{ \sqrt{x^2-6x-16} }{ \sqrt{x^2-12x+11} } \\ \left \{ {{x^2-6x-16 \geq 0} \atop {x^2-12x+11>0}} \right. " align="absmiddle" class="latex-formula">

$x^2-6x-16 \geq 0$
Определим нули функции
$x^2-6x-16=0$
Находим дискриминант
$D=b^2-4ac=(-6)^2-4*1*(-16)=100; \sqrt{D} =10$
Дискриминант положителен, значит уравнение имеет 2 корня
Воспользуемся формулой корней квадратного уравнения
$x= \frac{-b^+_- \sqrt{D} }{2a} \\ x_1= \frac{6+10}{2*1} =8 \\ x_2= \frac{6-10}{2*1}=-2$

0" alt="x^2-12x+11>0" align="absmiddle" class="latex-formula">
Определим нули функции
$x^2-12x+11=0$
Находим дискриминант
$D=b^2-4ac=(-12)^2-4*1*11=144-44=100; \sqrt{D} =10$
Дискриминант положителен, значит уравнение имеет 2 корня
Воспользуемся формулой корней квадратного уравнения
$x= \frac{-b^+_- \sqrt{D} }{2a} \\ x_1= \frac{12+10}{2*1} =11 \\ x_2= \frac{12-10}{2*1}=1$

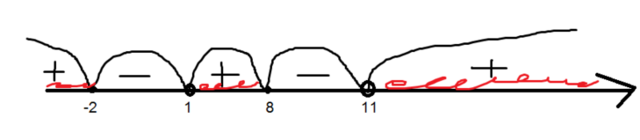
Знаки на промежутке смотреть во вложения

Ответ: $(-\infty;-2]U(1;8]U(11;+\infty)$