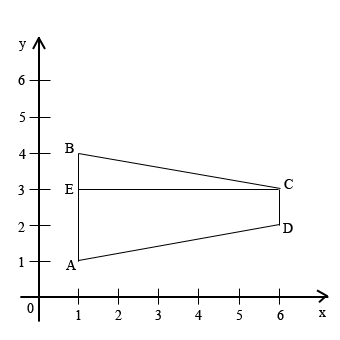
Отмечаем на координатной плоскости точки и соединяем их (смотри рисунок). Обозначим точки:
А(1;4), B(6;3), C(6;2), D(1;1). Основаниями трапеции будут AD и BC.
1) Проведем высоту из точки B. Обозначим ее BE.
Формула площади трапеции: S = ((BC + AD) / 2) * BE.
2) Находим длину AD: т.к. AD параллелен оси y, то длина AD = 4 - 1 = 3 (единицы)
3) Находим длину BC: т.к. BC параллелен оси y, то длина BC = 3 - 2 = 1 (единица)
4) Площадь: S = ((1 + 3) / 2) * 5 = 10 (квадратных единиц)
Ответ: площадь трапеции S = 10 (квадратных единиц).