Решаю, которые слева (←)
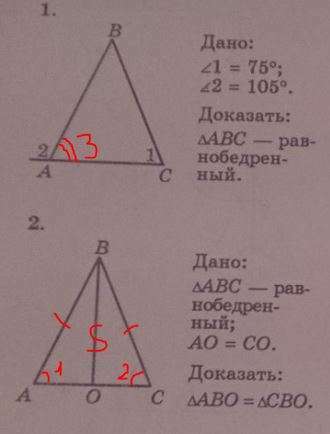
1. Дано: <1 = 75°, <2 = 105°<br>Доказать: ΔABC - равнобедренный.
Доказательство: Что мы знаем о равнобедренных треугольниках? Например, то, что две стороны в нём должны быть равны. Или то, что углы при основании равны. Именно второе и будем доказывать.
Нам даны 2 угла: <1 - угол при основании, <2 - внешний угол при основании. Т.к. <2 внешний, значит, он смежный с <3, а сумма смежных углов равна 180°, т.е. <2 + <3 = 180° ⇒ <3 = 180° - <2 =180° - 105° = 75°. Выяснилось, что <3 = 75°. Следовательно, <1 = <3 = 75 °. Значит, углы при основании равны. <br>
2. Дано: ΔABC - равнобедренный, AO=OC
Доказать: ΔABO = ΔCBO
Доказательство: Мы знаем, что в равнобедренном треугольнике 2 стороны равны, на данном рисунке, по идее, равны AB=BC. Ещё углы при основании равны, т.е. <1 = <2. Так же по условию AO=OC. И ещё, сторона BO является общей для обоих треугольников. ⇒ ΔABO = ΔCBO по I признаку ( <1 = <2 - как углы при основании, AO=OC - по условию, BO - общая).<br>