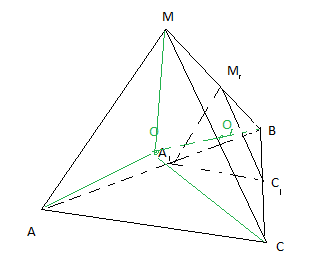
Дан правильный тетраэдр МАВС. Все его ребра равны.
АВ=АС=ВС=МА=МВ=МС=√6/2.
Через точку А₁ на ребре АВ, АА₁=А₁В в плоскости треугольника АМВ проведем прямую параллельную прямой АМ. Получим точку М₁, лежащую на ребре МВ, такую, что ММ₁=М₁В. АМ || A₁M₁. Через точку М₁ в грани МВС проведём прямую параллельную МС. Получим точку С₁ на ребре ВС, так что ВС₁=С₁С. МС || М₁С₁
Соединим точки А₁ и С₁, получим треугольник А₁С₁М₁ - нужное нам сечение.
Причем А₁С₁ || AC, так как является средней линией треугольника АВС.
Каждая сторона треугольника А₁М₁С₁ является средней линией треугольника АМС и А₁М₁=А₁С₁=М₁С₁=√6/4
Чтобы найти расстояние между плоскостями АМС и А₁М₁С₁ опустим перпендикуляр из точки В на плоскость АМС. Так как дан тетраэр, то вершина В проектируется в центр окружности, описанной около правильного треугольника АМС
ОА=ОС=ОМ=R
Аналогично точка О₁ - центр окружности, описанной около правильного треугольника А₁М₁С₁
О₁А₁=О₁С₁=О₁М₁=R/2 в силу подобия треугольников АМС и А₁М₁С₁ с коэффициентом подобия 2.
радиус окружности описанной около равностороннего треугольника можно найти по формуле

при a=√6/2 получаем R=√6/2 ·√3/3=√2/2
Тогда по теореме Пифагора ВО²=АВ²-АО²=(√6/2)²-(√2/2)²=6/4 - 2/4=4/4=1
Значит ВО₁=1/2 в силу подобия
и ОО₁=ВО-ВО₁=1/2
Ответ 1/2