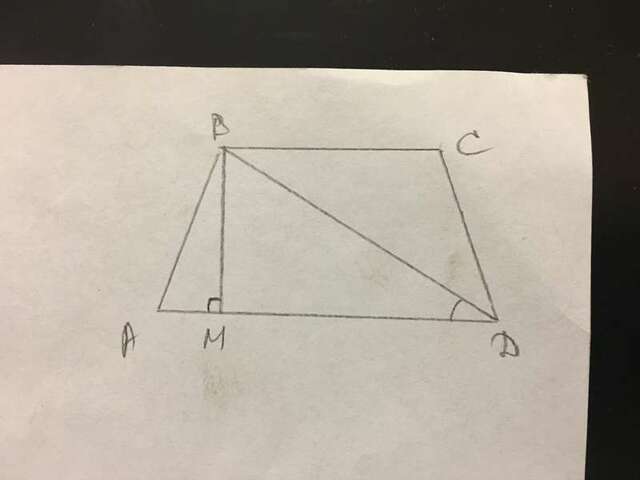
∠АВС=120°, ВМ⊥ВС, значит ∠АВМ=120-90=30°.
Высота в прямоугольном треугольнике, проведённая гипотенузе, делит его на два подобных ему треугольника так как каждый из них прямоугольный и имеет с большим треугольником общий острый угол.
Треугольники АВМ и АВД подобны, значит ∠ВДА=30° ⇒ АВ=АД/2=12/2=6 см.
В тр-ке АВМ ∠АВМ=30° ⇒ АМ=АВ/2=6/2=3.
ВМ²=АВ²-АМ²=6²-3²=27,
ВМ=3√3 см.
В равнобедренной трапеции ВС=АД-2АМ=12-2·3=6 см.
S=ВМ·(АД+ВС)/2=3√3·(12+6)/2=27√3 см² - это ответ.