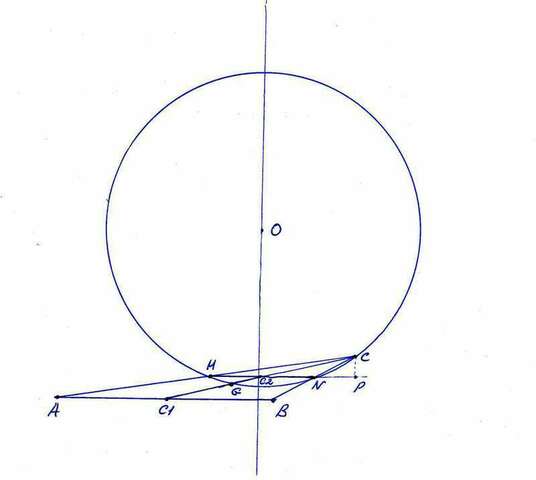
Я постарался нарисовать максимально близко к условию.
Окружность проходит через точку G на медиане CC1, 2*C1G = CG; и через концы средней линии MN. Так как точка C2 (пересечения MN и CC1) лежит посредине CC1, то GC2 = CG - CC2 = CC1*(2/3) - CC1*(1/2) = CC1/6 = CC2/3;
Если обозначить GC2 = q; то CC2 = 3*q;
Пусть также MC2 = NC2 = m; (по условию m = 1); R - радиус окружности, R = 41/9;
CP = y; C2P = x; C2O = d; по смыслу y = h/2; h - высота треугольника ABC;
1) по свойству пересекающихся хорд MC2*NC2 = CC2*GC2; или m^2 = 3*q^2;
2) OC^2 = C2P^2 + (C2O - CP)^2; или R^2 = x^2 + (d - y)^2;
3) C2N^2 + C2O^2 = ON^2; или R^2 = d^2 + m^2;
4) C2C^2 = C2P^2 + CP^2; или q^2 = x^2 + y^2; откуда 3*m^2 = x^2 + y^2;
Из 2) получается R^2 - d^2 = x^2 + y^2 - 2*d*y; или, с учетом 3) и 4)
m^2 = 3*m^2 - 2*y*d;
То есть y*d = m^2;
Дальше уже нет смысла "тащить" формулы в общем виде. Из 2) легко найти d = 40/9; (тут Пифагорова тройка 9,40,41), и получается y = 9/40; h = 9/20;
Площадь ABC S = 4*(9/20)/2 = 9/10;