1) Средние линии треугольника вдвое меньше параллельным им сторонам, значит стороны тр-ка АВС в два раза больше сторон тр-ка CНР и равны 24, 18 и 16.
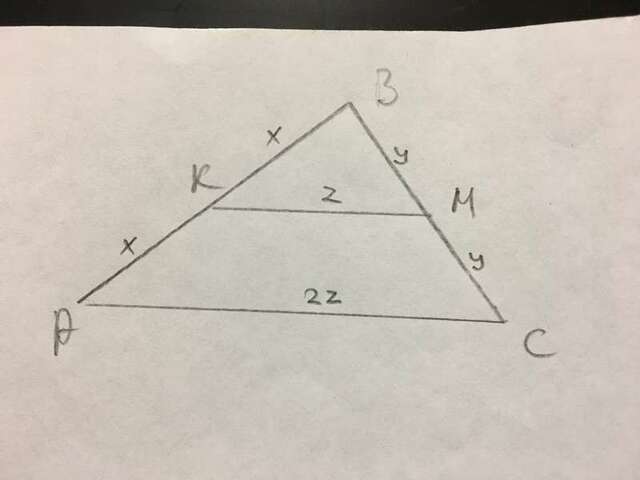
2) Введём условные обозначения как показано на рисунке.
P(KBM)=x+y+z,
Р(АКМС)=х+у+3z.
Р(АКМС)-P(KBM)=x+y+3z-x-y-z=6,
2z=6 см.
Р(АКМС)/P(KBM)=(x+y+3z)/(x+y+z)=5/3,
3x+3y+9z=5x+5y+5z,
2x+2y=4z=2·2z=2·6=12 см.
Р(АВС)=2х+2у+2z=12+6=18 см. - это ответ.