В прямоугольном треугольнике ABC с прямым углом C медианы CC1 и BB1 перпендикулярны друг...

Question

В прямоугольном треугольнике ABC с прямым углом C медианы CC1 и BB1 перпендикулярны друг другу. Найти длину большей из этих медиан, если длина третьей медианы AA1 = 3 корень из 3.

Answer 1

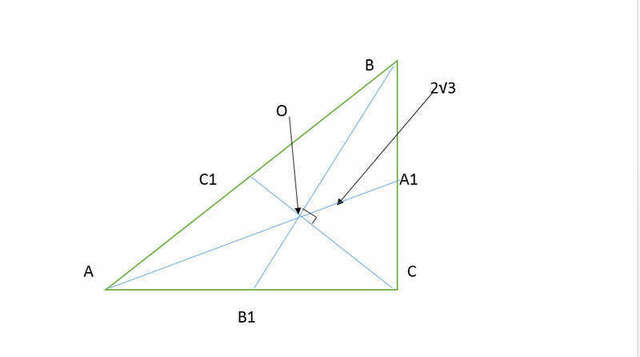
AA1 = 2√3
OA1 = (2√3)/3
OA1 = A1B = A1C
A1B = (2√3)/3
A1C = (2√3)/3

BC =A1B + A1C = 2*(2√3)/3 = (4√3)/3

AA1² = AC²+ A1C²

(2√3)² = AC² + ((2√3)/3)²

AC² = (2√3)² - ((2√3)/3)²
(2√3)² = 4*3 = 12
((2√3)/3)² = (2/√3)² = 4/3

AC² = 12 - 4/3 = 32/3

AC = √(32/3)

AC = AB1 + CB1
AB1 = CB1
AC = 2*CB1
CB1 = AC/2


BB1² = BC² + CB1²
BB1² = BC² + (AC/2)²

BB1² = ((4√3)/3)² + (√(32/3)/2)²
((4√3)/3)² = (4/√3)² = 16/3
(√(32/3)/2)² = (32/3)/4 = 8/3


BB1² = (16/3)² + (8/3)²=(2²*8²)/9+8²/9 =
= 8²(2²+1)/9 =8²*(5)/9

BB1 = √(8²*(5)/9) = (8*√5)/3
Ответ : длина большей из этих медиан BB1 =  (8*√5)/3
смотри рисунок

---

Comments

почему АА1 = 2 корень из 3, если по условию 3 корень из 3, а ответ должен быть 3 корень из 3

---

ой извини ответ не 3 корень из 3, а 3 корень из 2