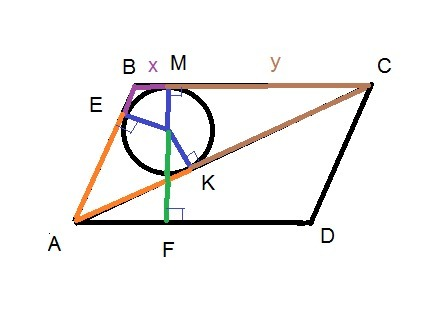
АВ,ВС и АС - касательные к окружности.
Касательные перпендикулярны радиусу, проведенному в точку касания.
OE⊥AB; OM⊥BC; OK⊥AC
OE=OM=OK=r=7
MF=MO+OF=7+8=15
По свойству касательных к окружности, проведенных из одной точки
BE=BM
CM=CK
AE=AK
По теореме Пифагора из Δ AOE
АЕ²=AO²-OE²
AE²=25²-7²
AE²=625-49
AE²=576
AE=24
AK=AE=24
Пусть BM=BE=x, CM=CK=y.
Тогда
Р( Δ АВС)= АВ+ВС+АС= (24+х)+(х+у)+(у+24)=2*(x+y+24)
S( Δ ABC)=p·r=(x+y+24)·7
S(параллелограмма)=ВС·MF=(x+y)·15
S(параллелограмма)=2·S( Δ ABC)
Уравнение:
(х+у)·15=2·(х+у+24)·7
х+у=336
ВС=х+у=336
S(параллелограмма)=(х+у)·15=336·15=5040
О т в е т. 5040 кв ед