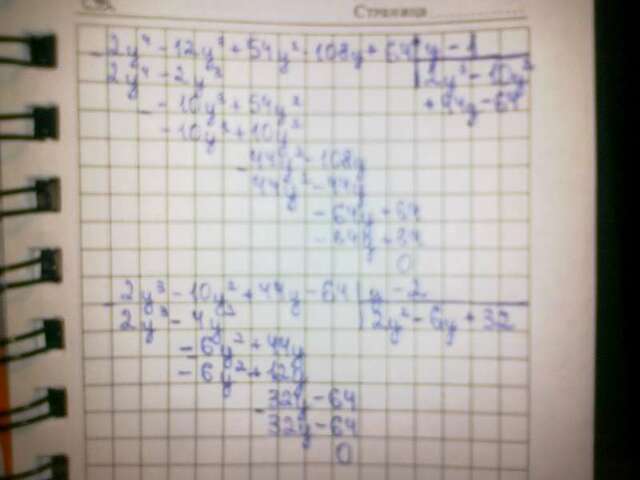x⁴+y⁴=17;
x+y=3;
Сразу видно, что подходят корни:
х₁=2; у₁=1;
х₂=1; у₂=2.
Но, можно и решить:
x⁴+y⁴=17; (1)
x=3-y; (2)
1. (81-108y+54y²-12y³+y⁴)+y⁴=17
2y⁴-12y³+54y²-108y+64=0
По схеме Горнера:
2y⁴-12y³+54y²-108y+64=(y-1)(2y³-10y²+44y-64)=(y-1)(y-2)(2y²-6y+32)
{2y²-6y+32=0; D<0.} ⇒ y₁=1; y₂=2;</em>
2. x₁=2; x₂=1.
Ответ: (2;1), (1;2).