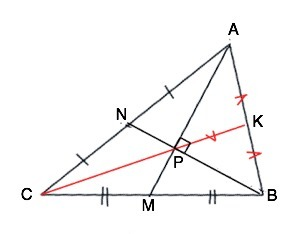
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
Продолжим СР до пересечения с АВ в точке К.
СК проходит через Р –точку пересечения медиан АМ и ВN, следовательно, СК - медиана, и СР=2 РК.
Треугольник АВР - прямоугольный, РК в нем – медиана.
В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы.
АВ=2 РК,
СР=2РК⇒ СР=АВ, что и требовалось доказать.