См. рисунок в приложении
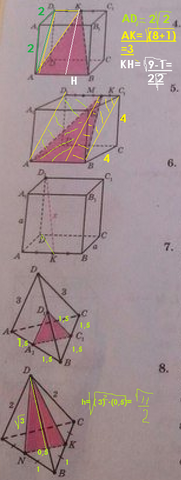
Задача 4
1) По теореме Пифагора диагональ грани
√(2²+2²)=2√2
2) По теореме Пифагора боковая сторона красного треугольника
√((2√2)²+1)=3
3) высота красного равнобедренного треугольника
√3²-1=2√2
4) S=1/2·2·2√2=2√2
ответ. с)
Задача 5.
Диагональ боковой грани √4²+4²=4√2
Площадь искомого треугольника равна половине площади прямоугольника с основанием ВС=4 и второй стороной ВС₁=4√2
S=1/2 ·4·4√2=8√2
ответ.b)
Задача 6
По теореме Пифагора ДК=√(а²+(а/2)²)=а√5/2
По теореме Пифагора
Д₁К=√а²+(а√5/2)²=3а/2
Задача 7
Треугольники подобны с коэффициентом подобия 1/2
Стороны искомого треугольника 1,5; 1,5 и 1,5
Площадь S= (1,5)²√3/4=9√3/16
ответ. а)
Задача 8
По теореме Пифагора
DN=√2²-1=√3
h=√(√3)²-(0,5)²=√3-(1/4)=√11/2
S=1/2·1·√11/2=√11/4
ответ. с)