х(3х-1)-х^2+16 ≤ х(2-х) -х(11-2х)
3х² - х - х² + 16 ≤ 2х -х² - 11х+ 2х²
2х² - х +16 -2х + х² +11х - 2х² ≤ 0
х² + 8х +16 ≤ 0
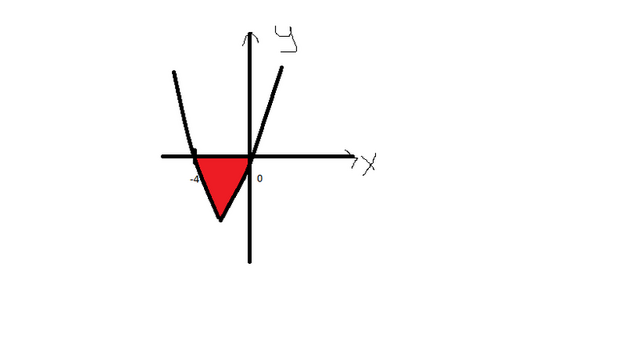
Рассмотрим функцию у = х² + 8х +16 Графиком функции является парабола, ветви направлены вверх т.к. k > 0
х² + 8х +16=0
D= 64 - 64 = 0, d=0 значит один корень, или два но они равны
х = -8 /2 = -4
Дальше по теореме виета
(х+4)(х+4)≤0
нф = 0, -4
Теперь можно или методом интервала или параболой, как понятно так и делай, я сделала параболой см во вложениях ( нам нужна закрашенная часть)
х∈ [-4, 0]