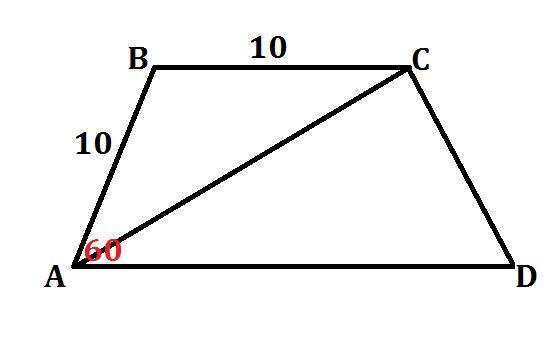
Ответ: R=10
Объяснение: Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
1) ∠B=120°
По теореме косинусов имеем:
AC²=AB²+BC²-2AB*BC*cos∠B
AC²=100+100+2*10*10*0.5
AC²=300
AC=10√3.
2) SΔABC= =
= =
=
3)