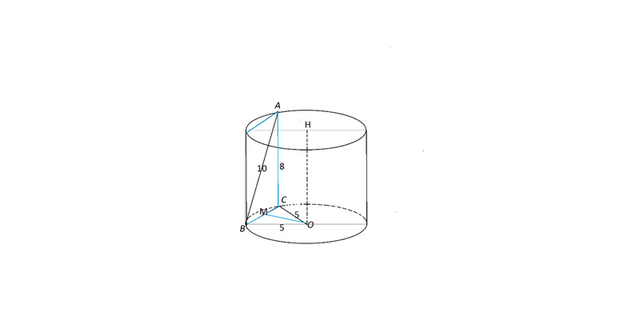
Отрезок AB, равный 10, упирается своими концами в окружности верхнего и нижнего оснований...

Question

Отрезок AB, равный 10, упирается своими концами в окружности верхнего и нижнего оснований цилиндра. Высота цилиндра равна 8, а радиус основания равен 5. Найдите расстояние между этим отрезком и осью цилиндра.

Answer 1

Отрезок AB, равный 10, упирается своими концами в окружности верхнего и нижнего оснований цилиндра. Высота цилиндра равна 8, а радиус основания равен 5. Найдите расстояние между этим отрезком и осью цилиндра.

Сделаем рисунок. 
 Из конца А отрезка АВ опустим перпендикуляр АС к  окружности нижнего основания. Соединив С и В,  получим хорду ВС - проекцию АВ на плоскость  нижнего основания.  
В прямоугольном треугольнике АВС  АВ - гипотенуза,  АС и ВС - катеты.  
Можно найти ВС по т. Пифагора. Но этот треугольник  египетский, можно сразу сказать, что ВС=6. 
 Соединим В и С с центром О основания.  
Треугольник ВОС - равнобедренный.  
МО - его медиана и высота, треугольник СМО -  прямоугольный.   
Радиус СО - гипотенуза этого треугольника, МС и МО  - катеты.  
МО=ВС:2=6:2=3
 И вновь египетский треугольник  с отношением  сторон 3:4:5
 МО=4.  ( можете проверить с т.Пифагора)

---

Comments

Добавлю,что отрезок АВ и ось ОН цилиндра - скрещивающиеся прямые. Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую. Плоскость АСВ, содержащая отрезок АВ, параллельна оси цилиндра ОН, т.к. АС и НО перпендикулярны плоскости основания. Следовательно, искомое расстояние - это длина отрезка МО.