6 задание,помогите пожалуйста ,математика 9 класс

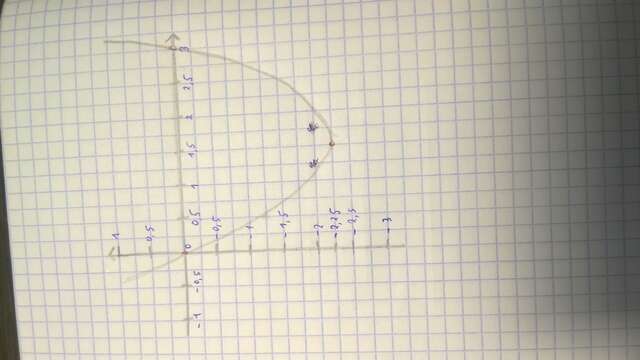
Ответ:

Чтобы нарисовать параболу, нужно действовать по пунктам

1) Указать направление веток

( $x^{2}$ - вверх, $-x^{2}$ - вниз)

2) Найти вершину параболы

(х вершину ищем по формуле $\frac{-b}{2a}$ и подставим х в уравнение)

3) Найти дополнительные точки

(Берем х = 0 и подставляем в уравнение, то же самое делаем с "у")

Решаем:

График: $x^{2}$ - 3x

1) Ветки направлены вверх.

$x = \frac{3}{2} = 1.5$

$y = 1.5^{2} - 3*1.5 = 2.25 - 4.5 = -2.25$

(1.5; -2.25)

$x = 0\\y = 0^{2} - 3 * 0 = 0$

(0; 0)

$y = 0\\x^2 - 3x = 0\\D = -3^{2} - 4*1 *0 = 9\\\\x_{1} = \frac{3 - \sqrt{9} }{2} = \frac{3 - 3}{2} = \frac{0}{2} = 0\\x_{2} = \frac{3 + \sqrt{9} }{2} = \frac{3 + 3}{2} = \frac{6}{2} = 3\\\\$

(0; 0), (3; 0)

Подставляем точки в график:

На фото.

Готово.