Ответ:
АВ = ВС = 21 см, АС = 30 см.
Объяснение:
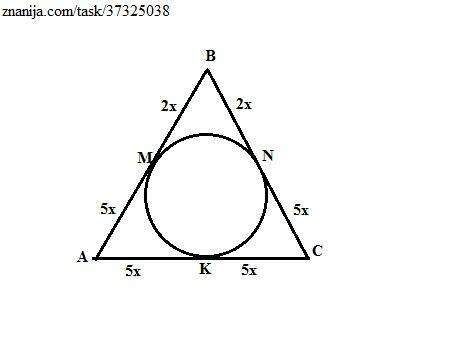
Отрезки касательных, проведенные из одной точки к окружности, равны (свойство). Пусть дан равнобедренный треугольние АВС с основанием АС. Точки касания вписанной окружности со сторонами АВ, ВС и АС - точки M, N и K соответственно. Тогда АМ = АК = КС = CN = 5х,
ВМ = BN = 2х. Периметр Pabc = 2·( 5x+2x+5x) = 72 см. =>
x = 3 см. => АВ = ВС = 7х = 21 см, АС = 10х = 30 см.