Ответ:
Пересечение (2; 3)
Объяснение:
В т. пересечения x и y одного круга = x и y другого круга. Т.е. для нахождения т. пересечения нужно решить систему уравнений
x² + y² – 8x – 4y + 15 = 0
x² + y² + 8x – 12y + 7 = 0
Умножим 1-ое уравнение на -1 и сложим
8x + 8x - 12y + 4y +7 - 15 = 0
16x - 8y - 8 = 0
разделим на 8
2x - y - 1 = 0
y = 2x - 1
Подставим полученное выражение для y в 1-ое уравнение:
x² + 4x² - 4x + 1 - 8x - 8x + 4 + 15 = 0
5x² - 20x + 20 = 0
разделим на 5
x² - 4x + 4 = 0
(x - 2)² = 0
x1 = x2 = 2
два корня совпадают, значит две точки пересечения совпадают, т.е. круги касаются друг друга.
y = 2x - 1 = 4 - 1 = 3
Точка касания x = 2; y = 3 или (2; 3)
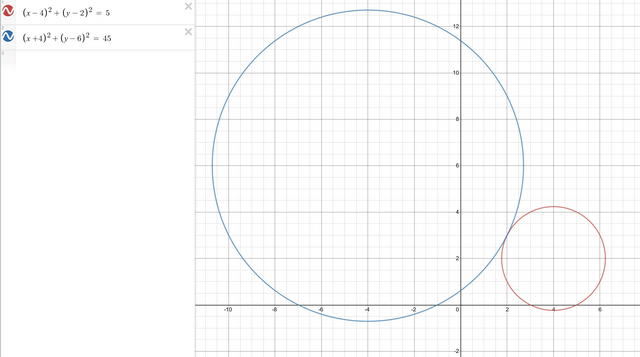
Данное решения можно проверить приведя уравнения окружности к стандартному виду и построив графики. см. рисунок.