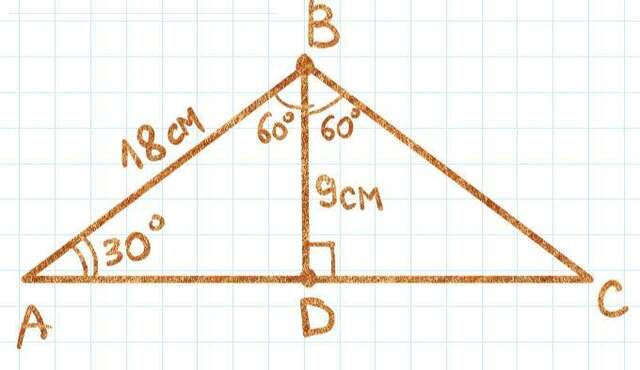
Дано:
ΔABC, AB = BC = 18 см
∠B = 120°
BD - медиана (D - середина AC)
Найти:
1) Углы Δ ABD
2) Длину отрезка BD
Решение:
см. чертеж!
Заметим, что в ΔABC: ∠A = ∠C = (180° - 120°) ÷ 2 = 30°
BD - медиана (по условию) ⇒ BD - высота и биссектриса (свойство равнобедренного треугольника) ⇒ ∠ADB = 90° и ∠ABD = 120° ÷ 2 = 60°.
1) Таким образом в ΔABD: ∠A = 30°, ∠B = 60°, ∠D = 90°
2) BD = 18 ÷ 2 = 9 см (как катет, лежащий против угла в 30°)