Ответ: решу кроме 5 и 8
Объяснение: задание 1
У каждого 4-х угольника сумма углов составляет 360°. Так как ромб- это правильный 4-угольник, то диагональ, которая проведена из вершины угла делит его пополам. И поэтому один из углов ромба полностью составит 24×2=48°. Угол, лежащий напротив него тоже составит 48°. Теперь найдём сумму 2-х остальных углов ромба: 360-(2×48)=360-96=264°
Итак: сумма 2-х других углов ромба составляет 264°. Теперь найдём каждый из них:
264÷2=132°; 2-й угол ромба =132°
Задача 2
sinA=DM/AD=20/25=4/5
Задача 3
Найдём площадь по формуле:
S=a×h, где h-высота параллелограмма, "а" - сторона, к которой проведена высота.
S=16×8=128см²; S=128см²
Задание 4:
Так как площадь квадрата - это произведение его сторон, то сторона квадрата равна √36=6см
Окружность и квадрат - это правильная фигуры, поэтому стороны квадрата соприкасаются с окружностью в симметрично расположенных друг от друга точек, во всех четырёх сторонах квадрата, поэтому найденная нами сторона квадрата будет равна диаметру окружности = 6см. Итак диаметр окружности будет 6см, тогда радиус будет 6÷2= 3см.
Радиус окружности 3см
Задание 6
Найдём периметр треугольника:
Р=41+41+18=100см; Р=100см
Теперь найдём площадь треугольника через пооупериметр:
Р/2= 100÷2=50см ; Р/2=50см
Теперь по формуле Герона:
S=√p(p-a)√(p-b)√(p-c), где р- полупериметр, a, b, c - стороны треугольника.
S=√50×√9×√9×√32=√129600=360см²
S=360см²; Р=100см
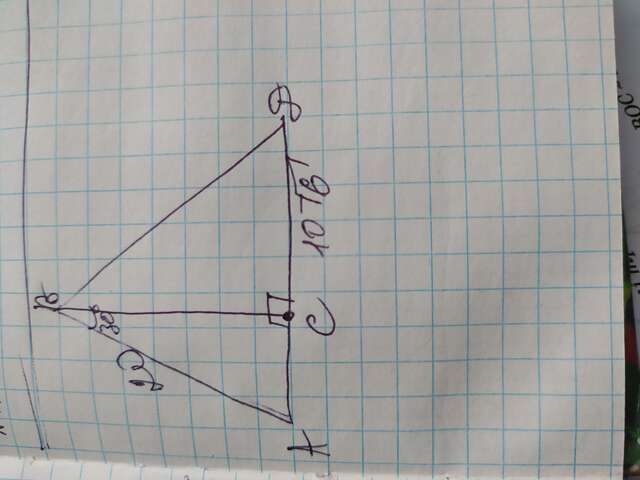
Задание 7:
Рассмотрим ∆АВС. Он является прямоугольным, также по условиям угол АВС= 30°, а катет, лежащий напротив него равен половине гипотенузы, и будет равен 20÷10=2
Мы нашли катет АС=10см
Теперь найдём по теореме Пифагора высоту ВС:
ВС=АВ²-АС²=√(20²-10²)=√(400-100)=√300=√100×√3=10√3. ВС=10√3см
Теперь найдём по теореме Пифагора искомую сторону ВД:
ВД=ВС²+СД²=(10√3)²+(19√6)²=√(300+600)=√900=30см
ВД=30см