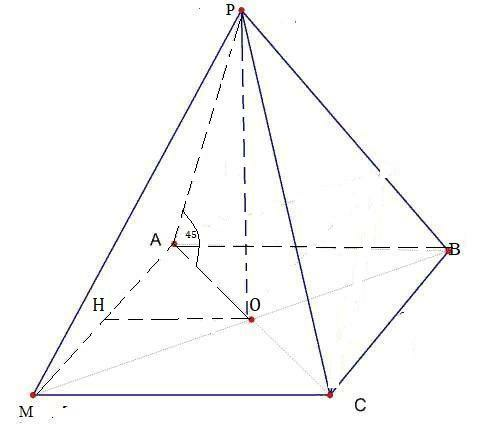
Боковое ребро правильной четырёхугольной пирамиды равно 8 см и образует с плоскостью основания пирамиды 45 градусов.
Найти: а)высоту пирамиды, б)площадь боковой поверхности пирамиды
Объяснение:
Пусть АВСМР-правильная 4-угольная пирамида , с основанием АВСМ, РА=8 см .
В правильной пирамиде вершина проецируется в центр основания ( т.О), т.е в точку пересечения диагоналей.Тогда углом между между боковым ребром и и плоскостью основания (АВС) будет ∠РАО=45°.
а) ΔАРО-прямоугольный, sin45°=РО/АР, √2/2=РО/8 ,РО=4√2 см.
И отрезок АО=4√2 см, т.к ΔАРО-равнобедренный ( ∠АРО=90°-∠РАО=90°-45°=45°).
б) S(бок.)=1/2Р(осн)*a, где а-апофема.
ΔАОМ-прямоугольный и АО=ОМ, по свойству диагоналей квадрата.
Значит по т. Пифагора АМ=√( (4√2)²+(4√2)²)=8 (см), АМ=АВ=ВС=СМ=8см.
Пусть ОН⊥АМ, тогда ОН=1/2АВ=4 см.
ΔОНР-прямоугольный , по т. Пифагора НР=√( РО²+ОН²)=√(16*2+16)=√16*3=4√3 (см). Значит а=4√3 см.
S(бок.)=1/2(4*8)*4√3=64√3 (см²)