Ответ:
81
Объяснение:
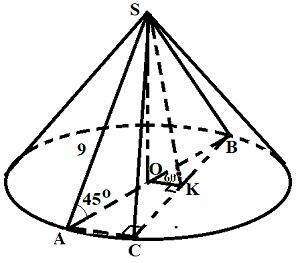
Так як в основу конуса вписано прямокутний трикутник, то гіпотенуза АВ трикутника є діаметром кола основи і відповідно висота конуса SO є висотою піраміди. Тоді кут SAO є кутом нахилу твірної до площини основи і дорівнює 45o за умовою. Проведемо перпендикуляр ОК до катета ВС (ОК||АС). Тоді за теоремою про три перпендикуляри SK також перпендикулярний до ВС і кут SKO є кутом нахилу бічної грані до площини основи і дорівнює 60o.
З прямокутного трикутника SAO AO=AScosA=9cos45o=, SO=ASsinA=9sin45o=. З прямокутного трикутника SKO KO=SOctgK= ctg60o==. Так як К- центр кола, то К - середина АВ і ОК - середня лінія трикутника АВС. Звідси АС=2ОК=. АВ=2АО=. З прямокутного трикутника АВС за теоремою Піфагора ВС2=AB2-AC2= =. Тоді ВС=. Знайдемо площу основи. S==. Об'єм піраміди V===81 .