Один из острых углов прямоугольного треугольника равен 60°, а сумма короткого катета...

Question

Один из острых углов прямоугольного треугольника равен 60°, а сумма короткого катета и гипотенузы равна 30 см. Определи длину короткого катета. 1. Величина второго острого угла равна 2. Длина короткого катета равна CM.

Answer 1

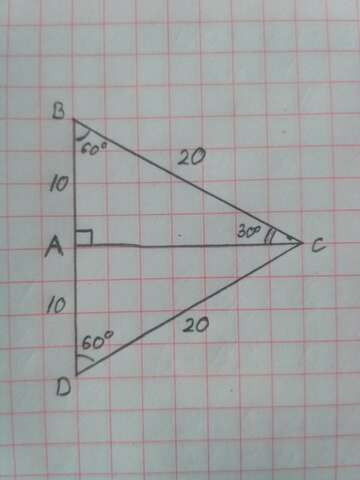
Пусть рассматриваемый треугольник ΔABC c прямым углом ∠BAC и углом ∠ABC равным 60°.

Тогда ∠BCA = 180°-∠BAC-∠ABC = 180° - 90°- 60° = 30°

Достроим ΔABC до равностороннего треугольника ΔBCD.

Тогда, так как сумма AB+BC=30см, то периметр ΔBCD= 30+30 = 60см

Так как ΔBCD равносторонний, то каждая его сторона равна

DB=BC=CD= 60:3 = 20см

Тогда сторона AB = BD:2 = 20:2 = 10см

Ответ:

Величина второго острого угла равна ∠BCA = 30°

Длина короткого катета равна AB = 10см.

---