Ответ:
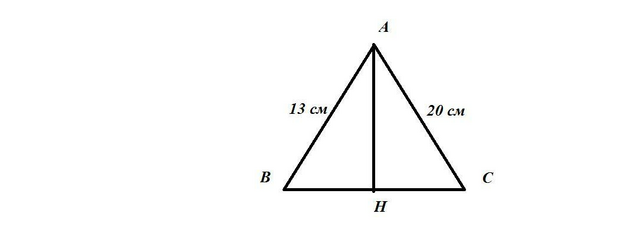
Пусть дан △АВС, из т.А к прямой b проходят две наклонные АС=20 см и АВ=13 см. Сумма проекций этих наклонных равна 21 см. Найдём проекции наклонных.
Рассмотрим △АВС : проводим высоту АН , образовано два прямоугольных треугольника АВН и АСН.
По т.Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы ⇒
1.) проекция наклонной
20²-х²=АН²
13²-(21-х)²=АН²
400-х²=169-(441-42х+х²)
400=169-441+42х
400=-272+42х
-42х=-272-400
-42х=-672
х=16 см
2.) проекция наклонной : 21 - 16 = 5 см