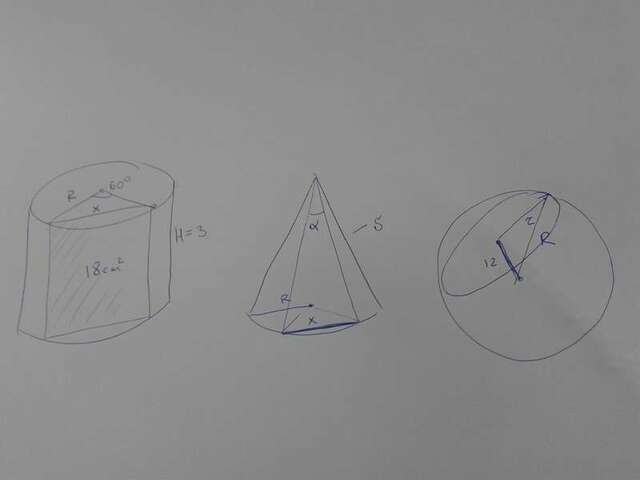
1. Площадь сечения Sсеч = H X = 18 (H высота X - хорда)
Хорда, которая опирается на угол 60 градусов X = 2 R cos 60 = R
значит Sсеч = R H
S=2 π R H = 2 π 18 = 36π
(тут получилось что образующая и не нужна, но если она равна 3 (это H) то X = 6. И радиус равен 6. )
2. S=π R L - площадь боковой поверхности
Если смотреть из вершины на хорду, получается треугольник, равнобедренный (L) с углом при вершине α в основании хорда.
По теореме косинусов хорда X² = L² + L² - 2 L L cos α = 2L²(1- cosα)
L = S/π/R
X = √2 √(1-cosα) L = √2 √(1-cosα) S / (πR)
3. Площадь сферы S = 4 π R²
Длина окружности L = 2πr = 10π ⇒ r = 5 дм
Далее из треугольника образованного радиусом сферы, радиусом сечения и расстоянием до центра (12 дм) радиус сферы R² = r² + 12² = 5² + 12² = 169
S = 4 π R² = 4 π 169 = 676 π