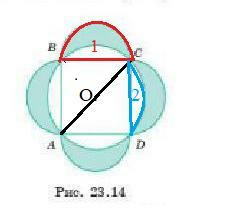
Объяснение:
Чтобы доказать , что площадь 4-х луночек Гиппократа равна площади квадрата, обозначим сторону квадрата а .
Выразим S(4 синих лун Г.).
S(4 синих лун Г.)=S(4 полукругов)-S( 4 сегментов2).
S( 4 сегментов2)=S(круга)-S(квадрата)
S( 4 сегментов2)=ПR²-а² ,т.к. R=( а²√2)2 вычисления ниже, то S( 4 сегментов2)=(Па²)/2-а² .
Найдем S(4 полукругов)=4*(1/2*П(а/2)² )=П(а²/2), т.к. радиус полугруга 1 равен а/2.
S(4 синих лун Г.)=П(а²/2)-( (Па²)/2-а² ) =П(а²/2)-(Па²)/2 +а² =а².
S( квадрата )=а².
Получаем S(4 синих лун Г.)=S( квадрата )
Доп. вычисления к задаче. ΔАВС-прямоугольный , по т. Пифагора АС²=ВА²+ВС² , АС²=2а² , АС=2√а. Радиус описанной окружности R=1/2АС⇒R=(2√а)/2