В треугольнике ABC медианы пересекаются в точке M. Через точку M, проведена прямая,...

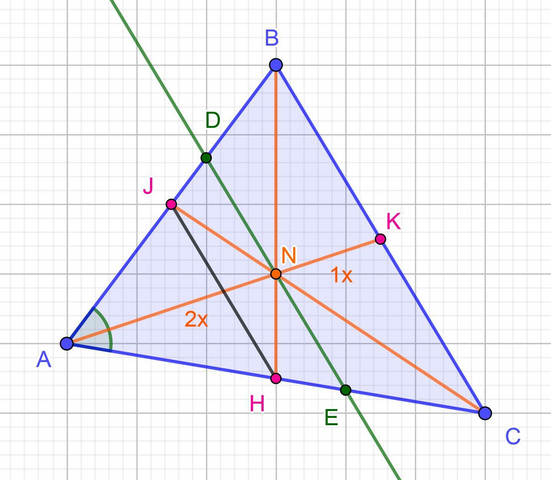
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

ΔDAN ~ ΔBAK по первому признаку подобия Δ-ов: ∠BAH — общий, DA:BA = EA:CA — за теоремой о пропорциональных отрезках.

У подобных фигур подобна и форма и внутренние элементы. Т.к. NA совпадает с медианой AK, значит и NA — медиана.

Коэффициент пропорциональности k = NA:KA = 2:3.

$\frac{DE}{BC} =\frac{2}{3} \\\\\frac{6}{BC} =\frac{2}{3} \:\: \Rightarrow \:\: BC = \frac{6\cdot 3}{2} = 9$

Ответ: Длина отрезка ВС равна 9.